研究紹介
メカトロニクス制御を数理最適化で究める
目標値追従性能と外乱抑圧性能を求められる応用先では,下図に示すようなフィードフォワード(FF)制御とフィードバック(FB)制御を組み合わせた2自由度制御に加え,学習制御を組み合わせた制御系が有効です。
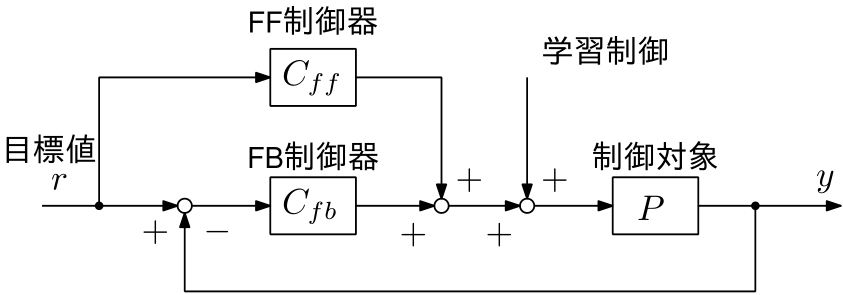
私達は,周波数応答データ駆動のフィードバック制御器設計,正確な逆モデルを実現するフィードフォワード制御器設計,反復学習制御による超高精度位置決めに加え,制御対象のシステム同定,目標軌道設計も行い,制御システムとしての統合最適化を目指しています。さらに,共同研究先と連携し,制御対象そのものの設計と制御系設計の統合最適化を目指しています。
また,先端制御技術を,直流遮断器や鉄道システムの制御に展開しています。
周波数領域システム同定
彼を知り己を知れば百戦殆からず[孫子, BC500]
を引用するまでもなく,制御対象についての知識を深めることは,制御性能を物理限界の上限近くまで引き上げるのに極めて重要です。
我々は,制御系設計に適した,Multisine信号の繰り返し加振と,ノンパラメトリックノイズモデルの活用を特徴とする周波数領域システム同定に関する研究開発をしています。MATLABツールボックスはGitHubに公開していますので,ご自由にお使いください。以下に活用例を示します。

機械共振を複数持つリニアモータによる位置決め装置で,FPD露光装置などの精密位置決めを模擬した装置です。位置センサを駆動側側(collocated side)と,負荷側(柔軟構造体の先,non-collocated side)の2つもっている1入力2出力系です。
これに対し,下式に示すMultisine信号と呼ばれる信号を繰り返し印加します。
\begin{align} u(t)=\sum_{i=0}^N A_i \sin \left(2 \pi f_i t+\phi_i\right) \end{align}
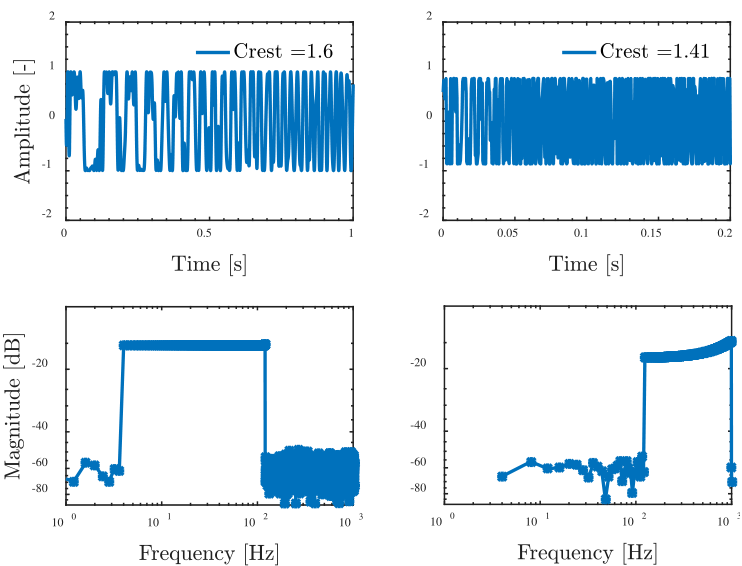
Multisine信号の特色は,任意の周波数成分とスペクトルを設計できることで,したがって制御対象のモード形状やS/N比に応じて加振信号を自由に設計(最適化)できることです。上図では,低・中域と高域の2つに周波数帯を区切った上で,さらに電流制御系の帯域の逆モデルを考慮した周波数重みにすることで,高周波域まで精度の高い同定を行います。これにより,有限の時間で最大限の情報を取り出すことができ,結果的に精度の高いノンパラメトリックモデル(周波数応答データ)を推定し,これをもとにパラメトリックモデル(伝達関数,状態空間モデル)を推定します。
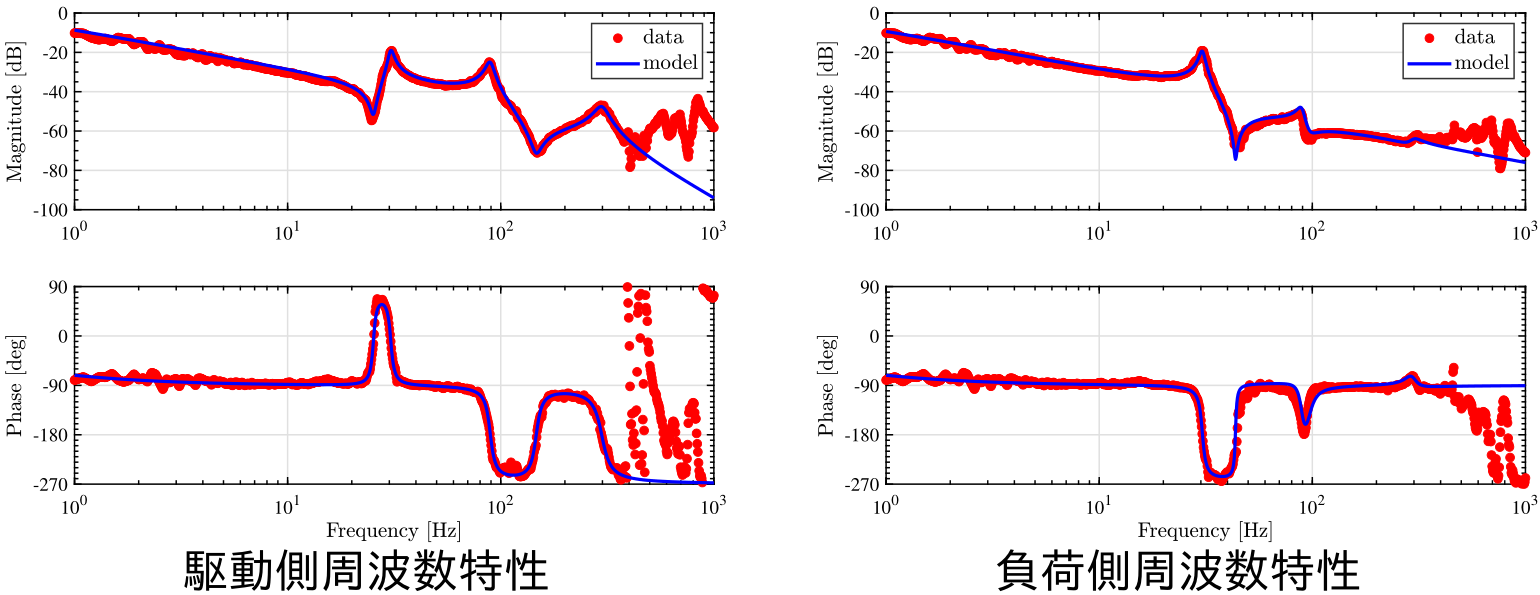
上図は,推定された周波数応答データとそこからフィッティングした1入力2出力の伝達関数です。分母多項式は同じであり,分子多項式のみを変えることで,剛体+3次モードまでの正確なモデル化に成功しています。分母多項式が共通ということは,状態空間表現した際に,1入力1出力系,1入力2出力系で$A$行列の次元が増加しないということで,オブザーバ・レギュレータの設計に有利になります。
また,正確なノンパラメトリックモデル(周波数応答データ)の取得は,フィードバック制御器のデータ駆動設計を容易にし,さらに正確なパラメトリックモデル(伝達関数・状態空間モデル)は,モデルベースフィードフォワード制御を容易にします。
周波数領域システム同定について,電気学会産業応用フォーラムにおいて,講習会を行いました。
フィードフォワード制御
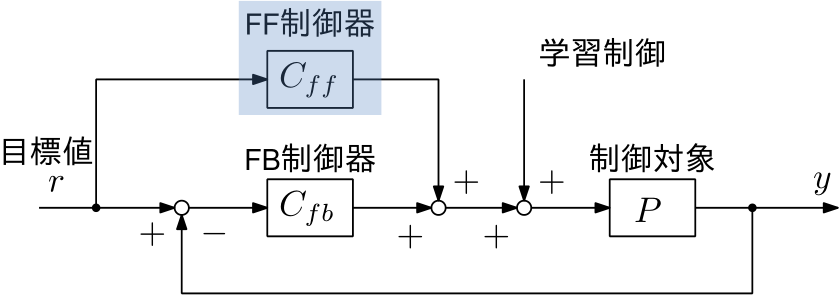
フィードバック制御器のみでは,目標値応答特性と外乱抑圧特性を独立に設計することができません。フィードバック制御器しか備えない場合,目標値応答特性と外乱抑圧特性のどちらかのせいで,どちらかの性能が妥協を強いられる場合があります。 例えば目標値応答特性において,制御入力が飽和するためにフィードバック制御のゲインを下げざるを得ない状況の場合,そのせいで外乱抑圧特性も低下することになります。
上記ブロック図において,感度関数を \begin{align} S=\frac{1}{1+P C_{fb}} \end{align} とするとき,目標値追従特性は下式で表されます。 \begin{align} y =\underbrace{P S u_{ff}}_ {\text{FF}}+\underbrace{P C_{fb} S r}_ {\text{FB}}= P S C_{ff}r+P C_{fb} S r \end{align} したがって, \begin{align} \frac{y}{r}=\frac{P C_{ff}+C_{fb} P}{1+C_{fb} P}, \quad \frac{e}{r}=\frac{r-y}{r}=\left(1-P C_{ff}\right) S \end{align} となります。ここで,フィードフォワード制御器$C_{ff}$を制御対象$P$の完全な逆系とするとき,すなわち$C_{ff}=P^{-1}$とすると \begin{align} \frac{y}{r}=1, \quad \frac{e}{r}=0 \end{align} が達成され,フィードバック制御器$C_{fb}$にかかわらず完全追従が可能になります。しかし,いくつかの点で厳密な意味での完全追従は困難です。
- 制御対象の正確なモデル化が難しい
周波数領域システム同定によって,$C_{ff}\simeq P^{-1}$ を目指します。しかしながら,プラント変動も考えるとこれには限界があります。この場合,上式から,追従誤差は感度関数$S$だけ圧縮されるので,やはり良好な感度特性(モデル化誤差が多い周波数で $S \to 0$,すなわちハイゲインフィードバック)を持つフィードバック制御器設計は重要です。 - 外乱応答により誤差が発生する
実際は$r$以外にも,入力端・出力端の外乱が存在し,$e=0$は達成できません。そのため,やはりフィードバック制御器は重要です。加えて,外乱に再現性がある場合,反復学習制御により反復して動作を行うなかで誤差を抑圧することが有効です。 - $P$ がプロパー,すなわち分子よりも分母の次数が高いため, $P^{-1}$が実装できない
これは,ローパスフィルタや多項式による滑らかな軌道生成により,数式的な純微分を行うことによって回避可能です。 - 不安定零点により,制御対象の逆系 $P^{-1}$が不安定極を持つ
これについては,不安定な逆系を,零振幅誤差追従制御(ZMETC),零位相誤差追従制御(ZPETC)等により安定な近似逆系を設計する手法が知られています。未来の指令値が既知であり,指令値が印加される前に制御入力を印加できる場合は,制御入力を事前に印加するPreactuationが非常に有用です。
Preactuationによる不安定零点に対する安定逆系の設計
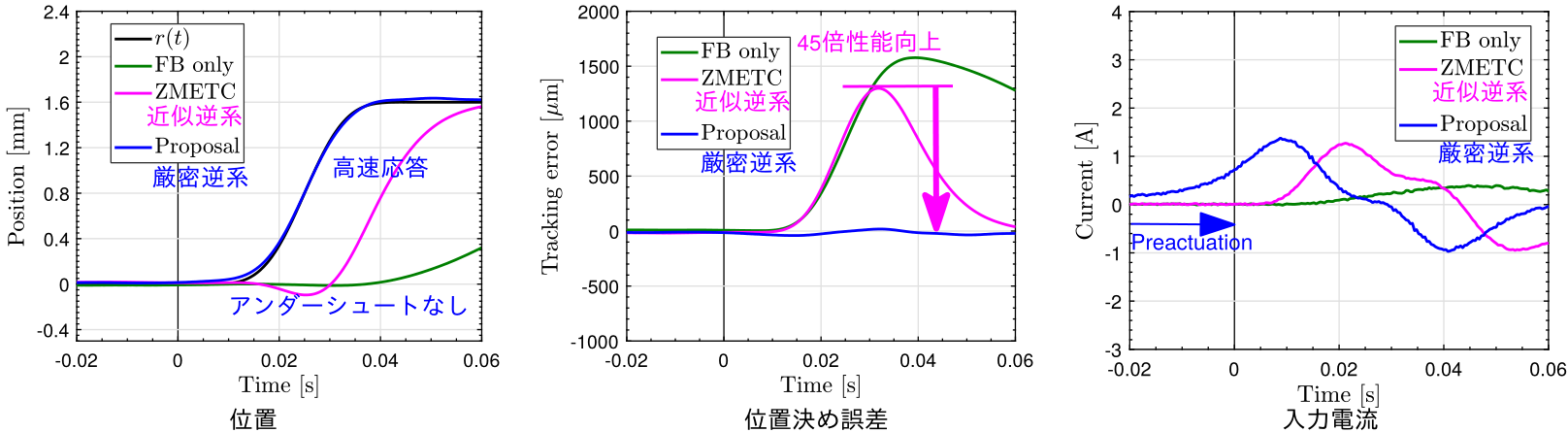
上図は,[Ohnishi, Beauduin, Fujimoto, IEEE/ASME Transactions on Mechatronics, 2019]の成果で,Preactuated multirate feedforward制御と言われる手法です。前項に示した位置決め装置と同定結果を用いた実機実験により,因果的な枠組のフィードフォワード制御法に対して,45倍も性能が向上しています。また,不安定零点がある系に対して発生してしまうアンダーシュートも大幅に抑圧できています。
この手法は,連続時間由来の零点(離散時間システムにおける真性零点)を時間軸反転を用いた安定逆系により設計し,離散化に由来する零点(離散化零点)をリフティングを用いるMultirate feedforward制御により設計する手法です。結果的に,状態変数軌道に対して$n$サンプル($n$は制御対象の次数)ごとに完全追従制御(PTC)を達成することができます。
出力追従制御 v.s. 状態追従制御
![]()
また,(Single-rate) stable inversion を含む通常の離散時間制御系は,制御入力$u$から出力$y$までを反転させるため,毎サンプル出力に追従(Output-tracking)しようとします。しかし,その場合は,サプル点間応答が悪化する場合があります。一方で,状態変数に追従(State-tracking)しようとするMultirate feedforward制御は,例えば上図の2次系の例では,出力位置だけでなく速度も追従しようとするため,結果的にサンプル点間応答が良好になっています[Ohnishi, Strijbosch, Oomen, International Journal of Robust and Nonlinear Control, 2022]。
また,Multirate feedforward制御法の次数を削減する試みとして,[Zundert, Ohnishi, Fujimoto, Oomen, IEEE/ASME Transactions on Mechatronics, 2020]を提案しました。
様々なフィードフォワード制御器の設計法とその比較について,電気学会産業応用フォーラムにおいて,講習会を行いました。
姿勢制御に対するMIMO非線形FF制御
FPD露光装置などの姿勢制御は,
- 動力学(オイラーの運動方程式)
- 運動学(座標系の回転)
の双方の非線形性と軸間干渉が存在します。
これに対する非干渉化をねらうMIMO非線形FF制御として,[大西, 藤本, 堀, 坂田, 鈴木, 佐伯, 電気学会論文誌D, 2014]を提案しました。この制御法は,3軸姿勢制御を行う,人工衛星やヘリコプターなどにも適用可能です。
目標軌道最適化
フィードフォワード制御器の設計は,前項で述べたように,本質的に逆システムはノンプロパーなため,滑らかな軌道を要求するために目標軌道生成と不可分です。
そこで,目標軌道生成に関するMATLAB Toolboxを開発し,GitHubで一般公開しています。
データ駆動フィードバック制御器自動設計
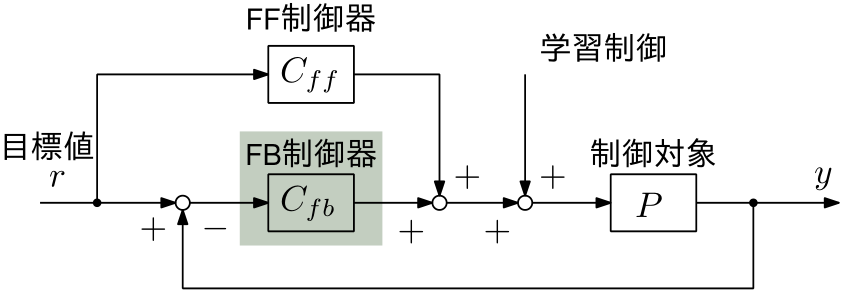
不安定な制御対象の安定化,そして外乱の抑圧のために,高性能なフィードバック制御器は不可欠です。 周波数領域システム同定によって得られた周波数応答データを直接用いて,非線形性最適化問題である制御器パラメタ決定問題に対して,(準)最適な解をデータ駆動で求める研究を行っています。
複数センサを活用するSRC-P-PI制御器の周波数応答データ駆動自動設計
前項に示した位置決め装置のように,精密位置決め装置では,例えばサーボモータ側のエンコーダに加えて,ステージ側のリニアエンコーダを持つフルクローズド制御が広く用いられています。 サーボモータ側のエンコーダは電流制御のみに用い,リニアエンコーダを摩擦やバックラッシュなどのロストモーション補償と最終位置決めのために用いる構成が広く使われています。
それに対し,[大西亘, 電気学会論文誌D, 2019]においては,駆動側エンコーダを速度制御,負荷側リニアエンコーダを位置制御するP-PI制御系に対し,主共振を相殺するSelf Resonance Cancellation (SRC)を組み合わせたSRC-P-PI制御系の周波数応答データ自動設計を提案しました。
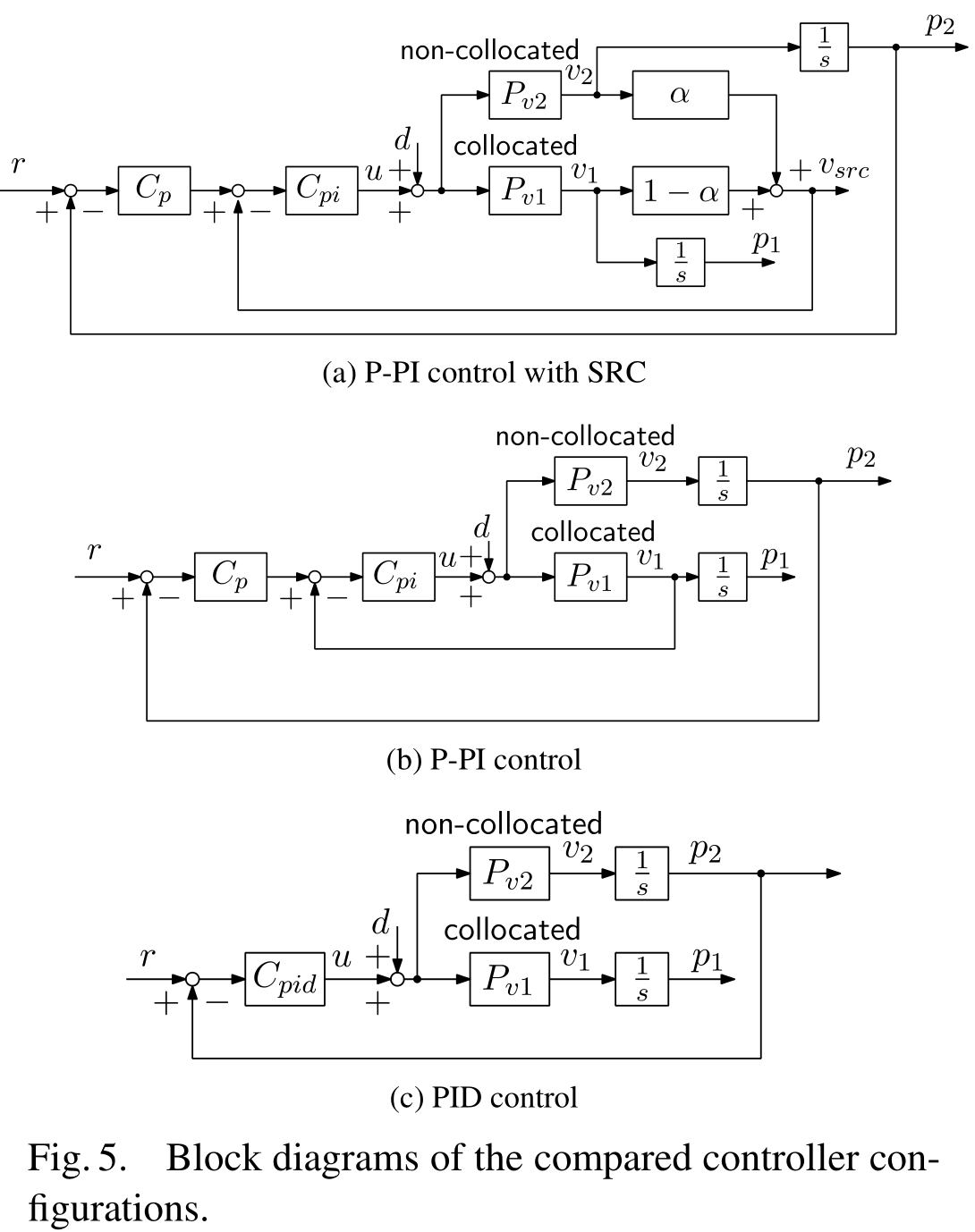
上図の3つの構成に対して,周波数応答データを直接活用する自動設計法を提案・適用しました。制御器設計問題は非凸最適化問題であるため,以下の手順で最適化を行い,「素性の良い」制御器を求めることを提案しました。
- 周波数応答データによるSRC制御器の内分比最適化
- 主共振が見えなくなった制御対象への低次パラメトリックモデルによる極配置設計による速度制御初期ゲイン導出
- 逐次線形化による速度制御ゲイン最適化
- 非線形最適化によるSRC内分比と速度制御ゲイン同時最適化
- 位置制御ゲイン最適化
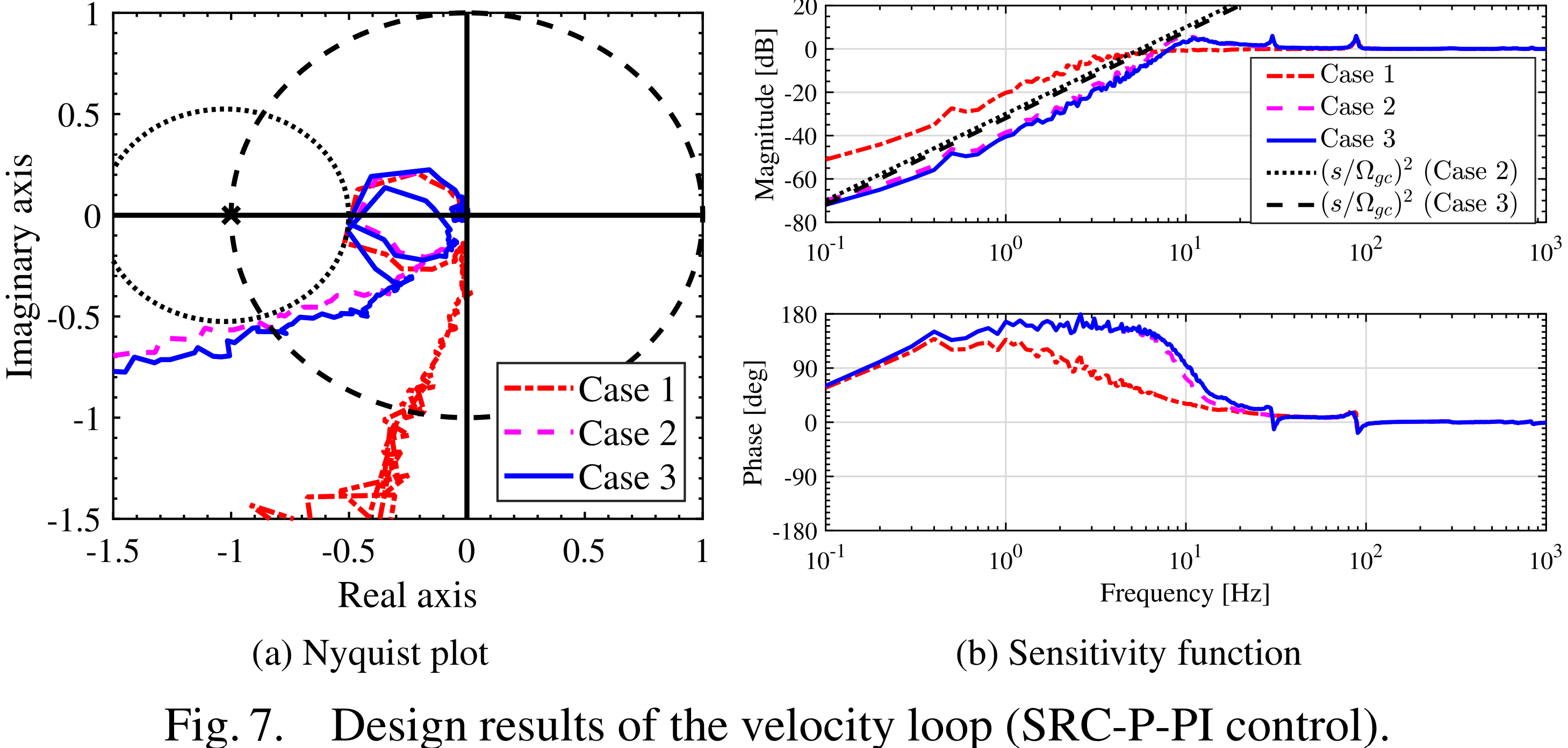
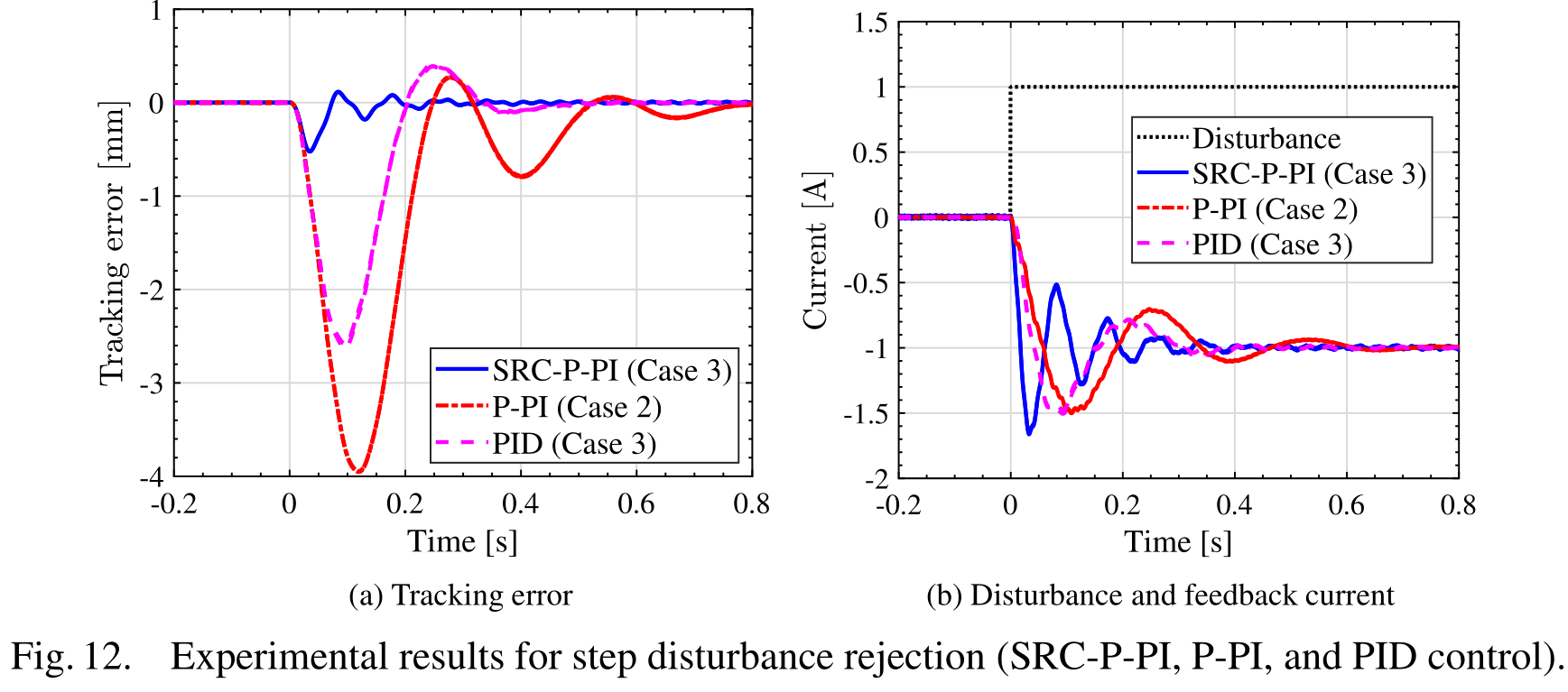
その結果が,上図Fig. 7とFig. 12で,周波数応答データを直接用いながら,制約を満たしつつ制御帯域の最大化に成功し,結果的に他の手法に対してかなり早い外乱抑圧を達成しました。
周波数応答データ駆動外乱オブザーバ最適設計
RCBode, RBodeの支援による自動設計
反復学習制御
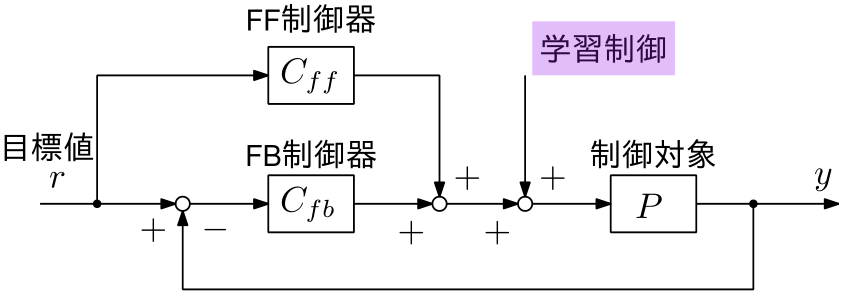
再現性のある外乱抑圧には,(反復)学習制御が非常に有効で,過去にも様々な研究が行われています[ref1][ref2][ref3]。
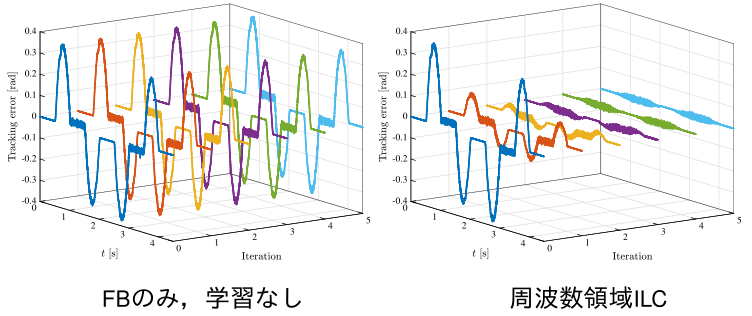
この手法は,上図のように,誤差が再現する場合,繰り返し動作を行うことで位置決め誤差が収束していくという手法です。特に周波数領域反復学習制御は反復領域の安定性が周波数応答データで判別可能なことから,周波数領域システム同定とも相性がよく,また制御パラメタ設計も直感的です。
状態追従型反復学習制御
![]()
そこで私達は,オランダEindhoven工科大学との共同研究で,フィードフォワード制御の枠組みだったMultirate feedforward制御による状態追従制御を,周波数領域反復学習制御に拡張[Ohnishi, Strijbosch, Oomen, International Journal of Robust and Nonlinear Control, 2022]しました。 上図のように,オブザーバによって状態推定し,それが状態変数軌道に対して追従するように学習を行います。
![]()
実験結果を上図に示します。 従来の出力追従型周波数領域反復学習制御は,前項に示した通り,サンプル点間応答が劣化する場合がありますが,提案手法は良好なサンプル点間応答を実現することから,一般的に使われている出力追従を目指す周波数領域反復学習制御に対して性能が凌駕していることがわかります。
機械学習と反復学習の融合
精密制御で半導体微細化を支える
FPD露光装置

上図は,FPD露光装置と呼ばれる巨大な装置で,スマートフォン,テレビ,PCのディスプレイを露光というプロセスにより回路パターンを刻む装置です。 動作は下のYoutubeをご参照ください。 Nikonとの共同研究によりFPD露光装置のステージの高速高精度位置決めを目指しています。
機構と制御の統合化設計による非干渉化
この装置のステージは, $x,y,z,\theta_x,\theta_y,\theta_z$ の6自由度を持ち,軸間干渉が問題となります。例えば,アクチュエータの高さと,ステージの重心点・回転中心の高さが一致していないと,自動車の急加速・急減速でのピッチング運動と同じく,並進運動(例: $x$)から回転運動(例: $\theta_y$)への軸間干渉が生じます。機械や構造的な制約により,これらを完全に一致させることは困難です。 そこで,新たに$x$軸方向に冗長にアクチュエータを配置したステージ構造を提案し,推力配分により制御側で推力点高さを変更できるステージ構造を提案しました。 さらに,重心点・回転中心・推力点・計測点の位置を陽に考慮したモデル化により,推力点と重心点を一致させた「重心駆動」は高周波域の軸間干渉を抑圧し,推力点と回転中心を一致させた「回転中心駆動」は低周波域の干渉を抑圧することを明らかにしました[Ohnishi,Fujimoto,Sakata,Suzuki,Saiki, IEEJ Journal of Industry Applications, Vol. 5, No.2, pp. 141-147, 2016.]。さらに,相補フィルタによる周波数分離により,低周波域では回転中心駆動,高周波域では重心駆動となる,「回転中心・重心点ハイブリッド駆動」を提案し,実験的に軸間干渉が下がることを示しました[大西, 藤本, 坂田, 鈴木, 電気学会論文誌D, 2019]。さらに,Direct Nyquist Array法を指標にした機構と制御の統合設計法により, $f_x \to \theta_y$だけでなく$\tau_y \to x$の干渉を低減させる手法を提案しました[Ohnishi, Fujimoto, Sakata, Suzuki, Saiki, American Control Conference, 2015]。
多入力多出力系に対するデータ駆動フィードバック制御器設計
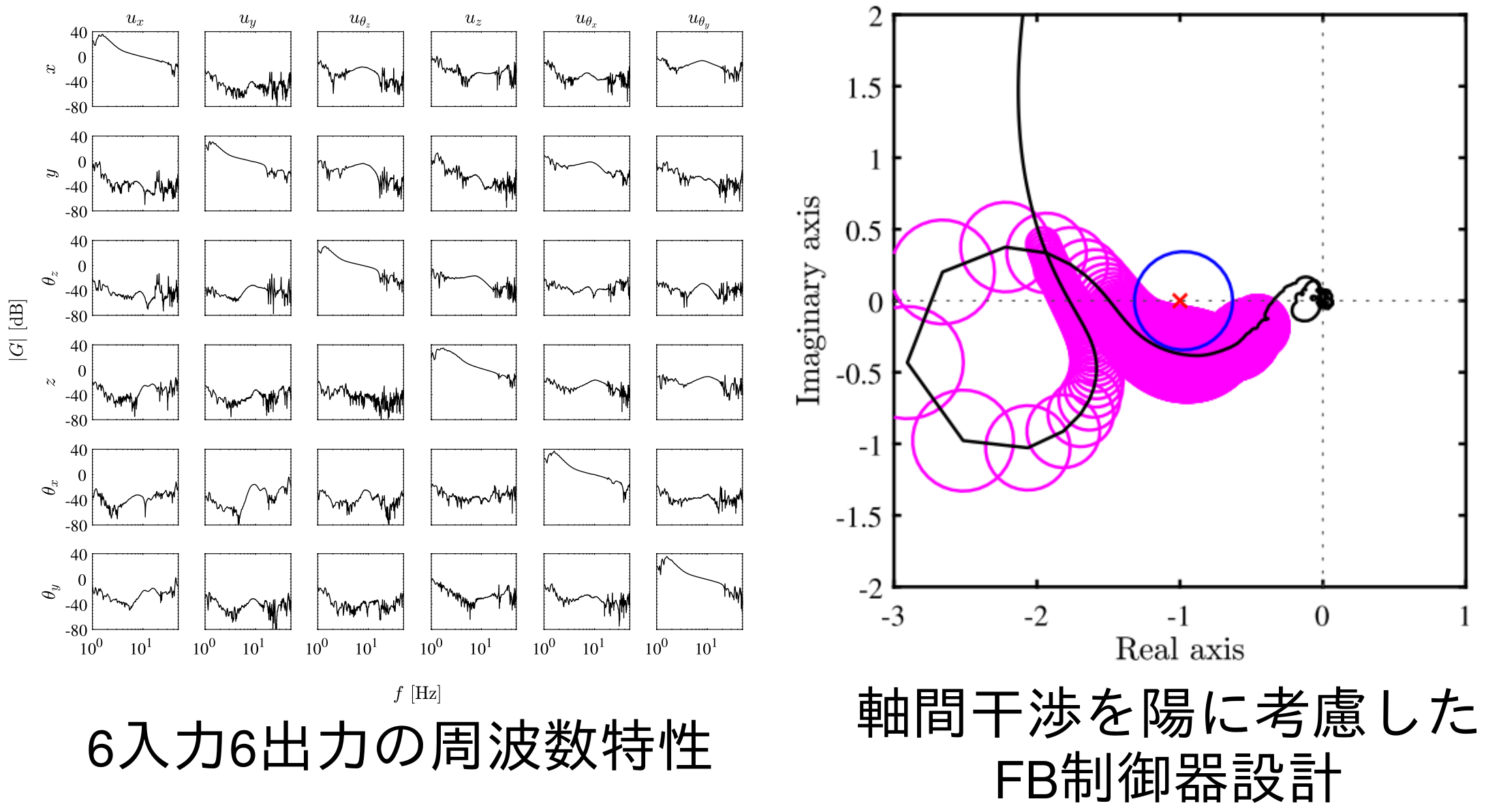
1軸の制御対象では,局所的な外乱を積極的に抑圧するピークフィルタ(逆ノッチフィルタ)がよく用いられています。しかし,FPD露光装置のステージは前述の通り軸間干渉を持つため,ピークフィルタによって多軸の性能が悪化する可能性があり,系統的な設計手順が存在しませんでした。さらに,試行錯誤的な設計は組合せ爆発する課題がありました。そこで[Mae,Ohnishi,Fujimoto,Sakata,Hara,Mechatronics,2022]においては,逐次線形化法をうまくMIMO系に適用することで,安定性を確保しつつ外乱抑圧性能を向上させることを提案し,さらに実際のFPD露光装置に実装し,有効性を実証しました。
空気圧アクチュエータによる精密制御
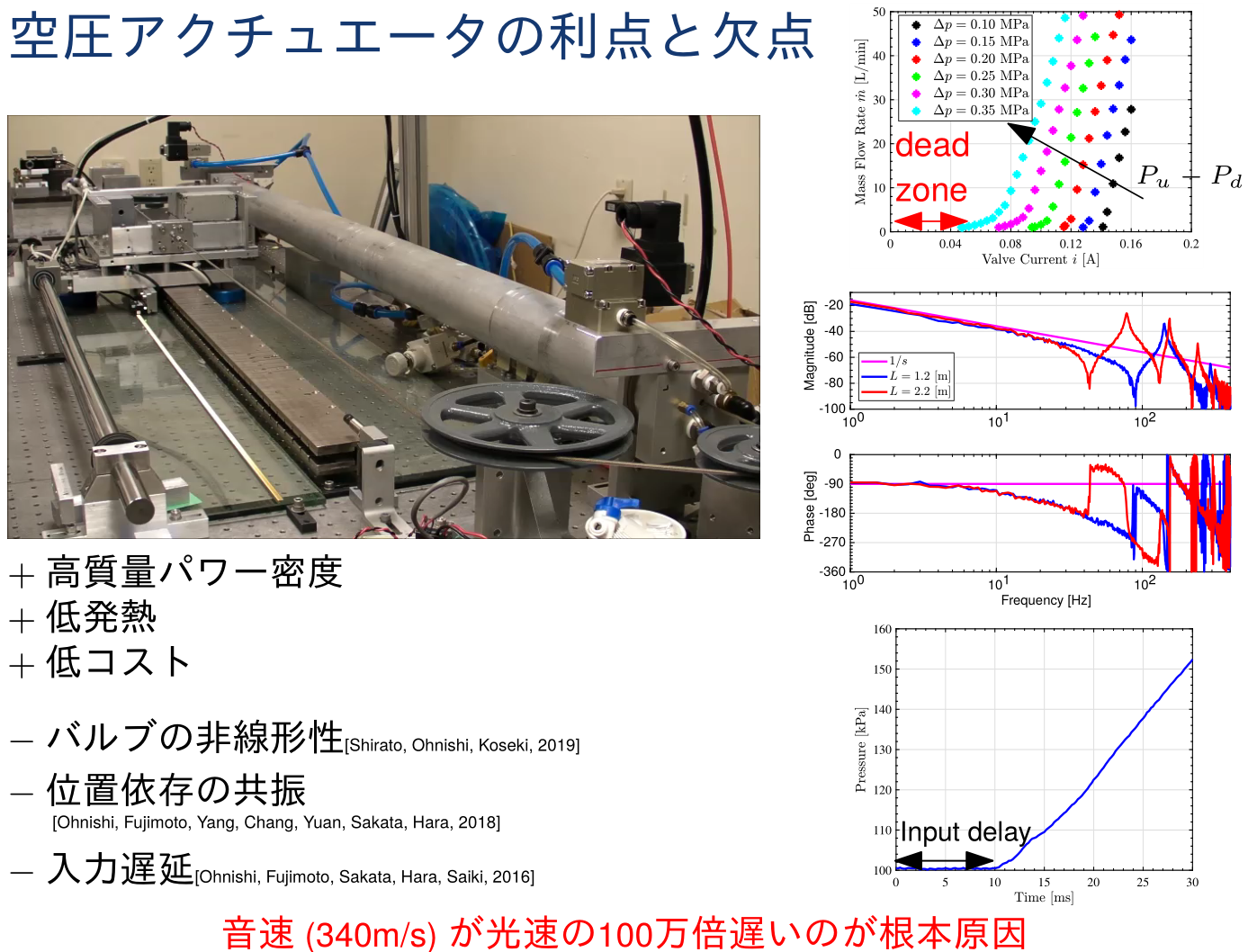
空気圧アクチュエータは,上図のような制御上の難しさがあるため,専ら低コストで位置決め精度が必要ない制御対象に用いられてきました。このうちの一つの課題は,本質的に空気の粗密波の伝播が遅いことに起因する波動モードによりステージ位置依存の共振が存在するということがあります。
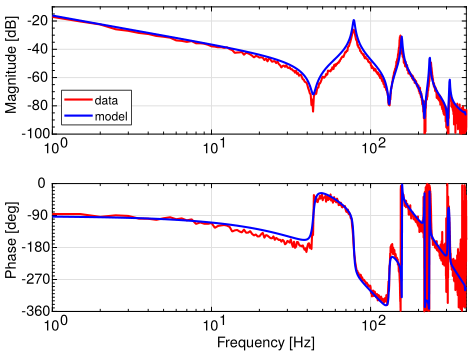
これに対し私達は,ダンピングも考慮できる「修正波動方程式」を提案し,上図のように良好なモデル化が可能であることを示しました。
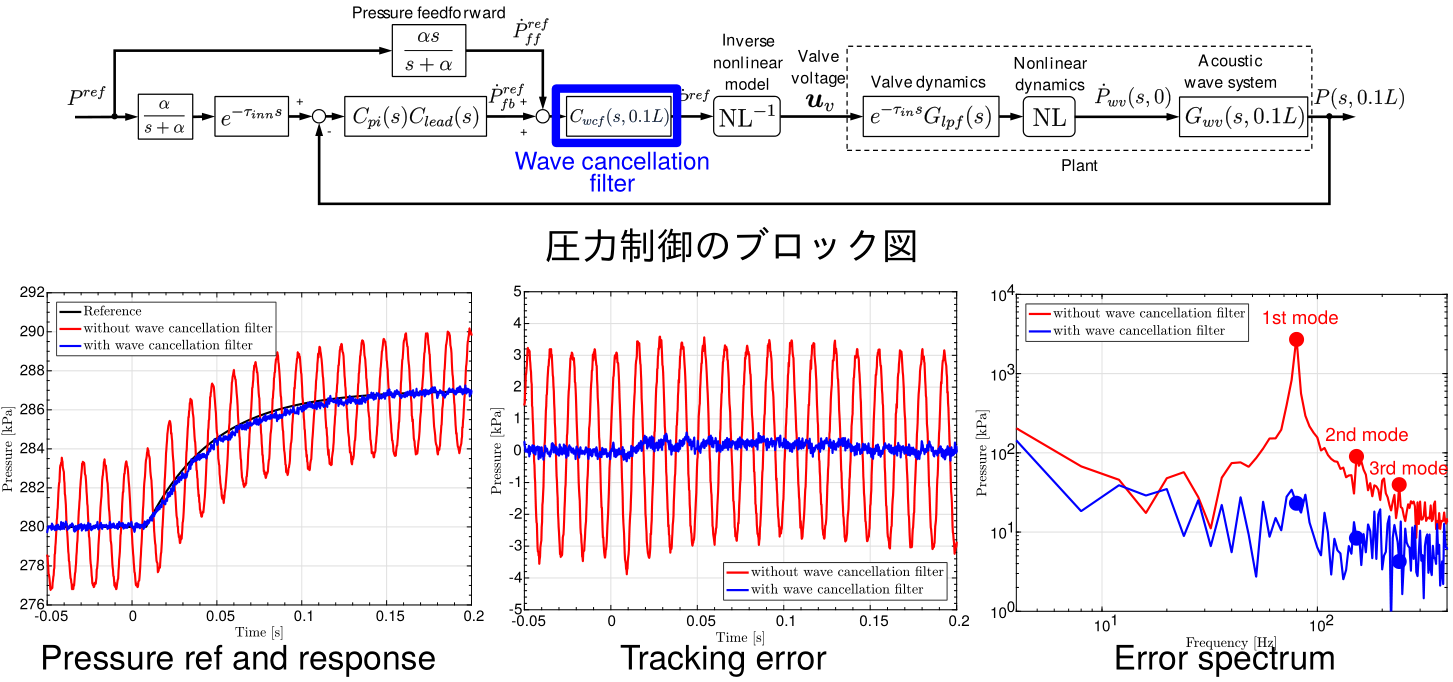
このモデルからフィルタを設計し,制御対象に直接に挿入することで,波動に関わるモードを「相殺」し,制御器からはまるで共振がない制御対象に見せる制御法を提案しました。 これにより,上図のように従来は存在した圧縮性に起因する共振がきれいになくなり,精密な圧力制御を実現しました。
半導体熱処理炉の温度制御
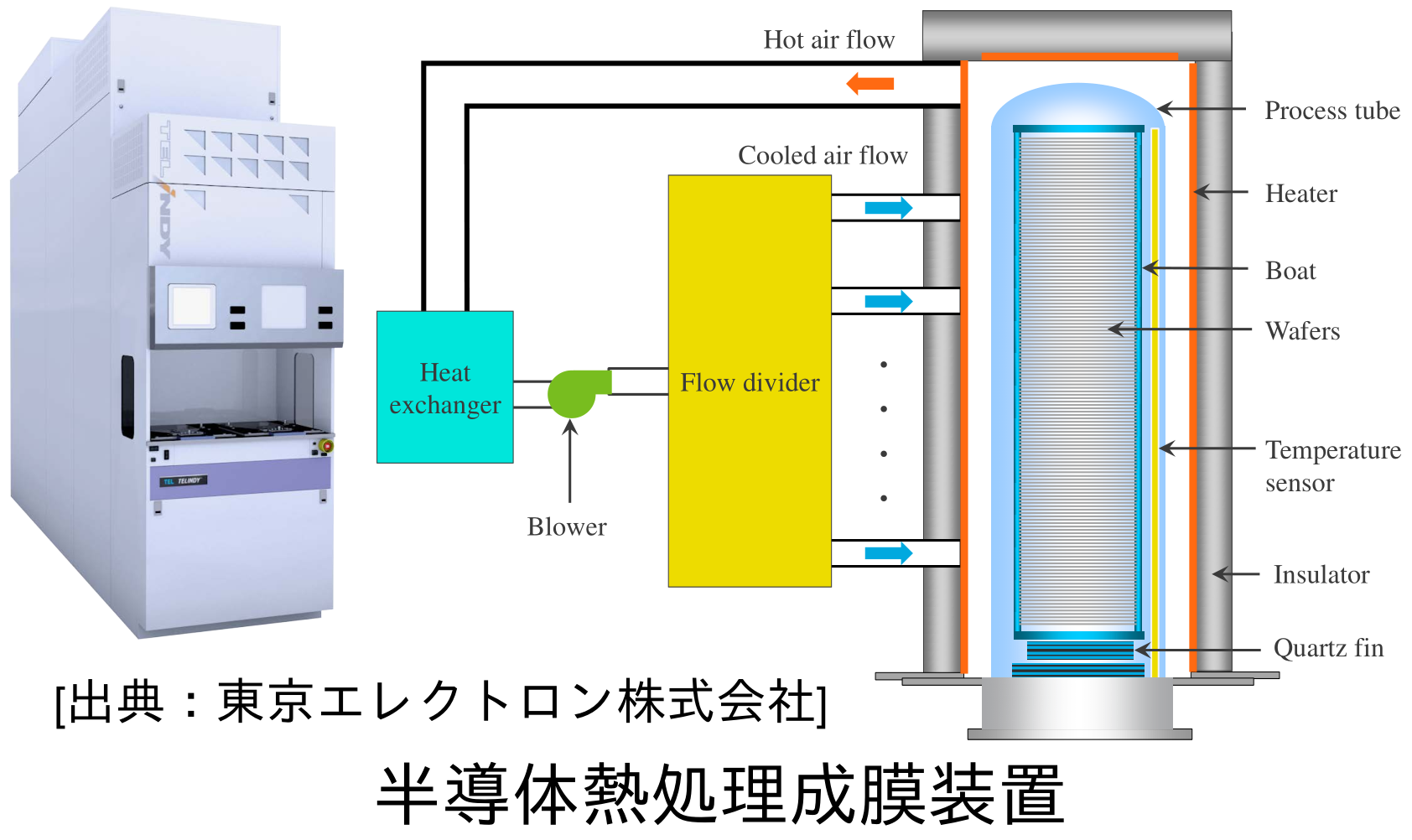
半導体集積回路の製造工程は多岐にわたり,露光の前後に熱処理工程があります。上図の半導体熱処理成膜装置(バッチ式熱処理炉)もその一つで,シリコンウェハを100枚以上同時に処理をすることができます。 この熱処理炉は,エネルギ効率向上のため,断熱性が向上しており,そのトレードオフとして自然冷却が遅くなってしまっています。したがって,アクティブ冷却装置を持つものも現れていますが,モータと違い,ヒータやクーラは正負を出力することができません。 また,従来のヒータとクーラを別々のアクチュエータとしてみなす最適制御では,その両者を同時に出力する場合があり,エネルギ効率が悪いという課題がありました。 この課題に対し,東京エレクトロン テクノロジーソリューションズ株式会社と共同研究を行いました。
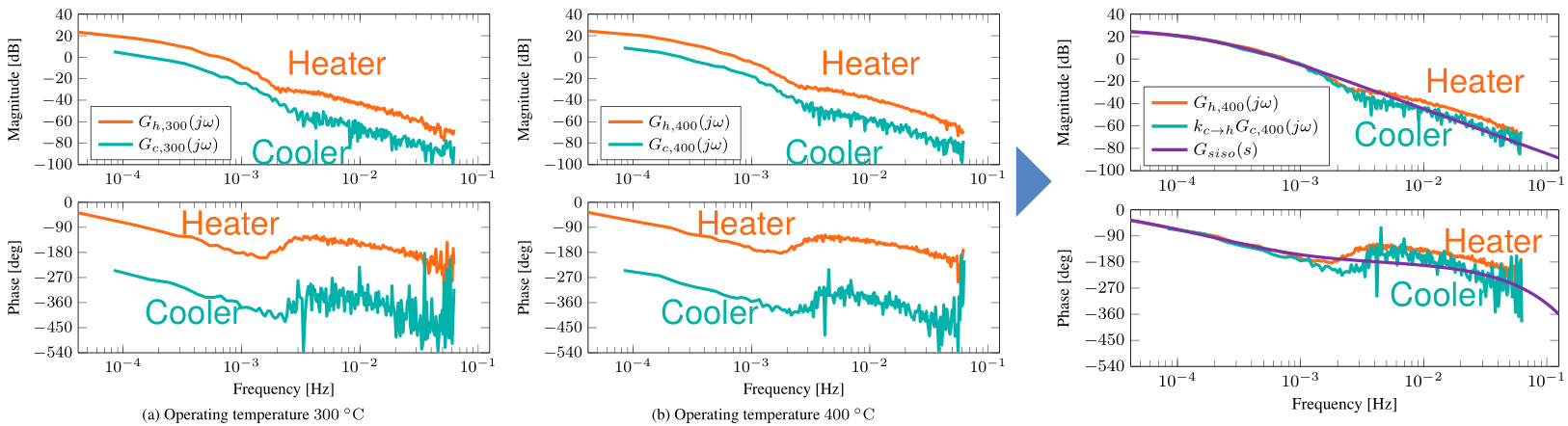
そこで,周波数領域システム同定を用いてヒータ・クーラから温度までの特性をモデル化すると,それらがゲインをかければ束ねられることが分かりました。これにより,正負の制御入力を出力する仮想的なアクチュエータとみなることができます。
これを用いて,フィードフォワード制御器,フィードバック制御器を持つ2自由度制御系を構築し,実際のバッチ式熱処理炉を用いて温度制御実験を行いました。
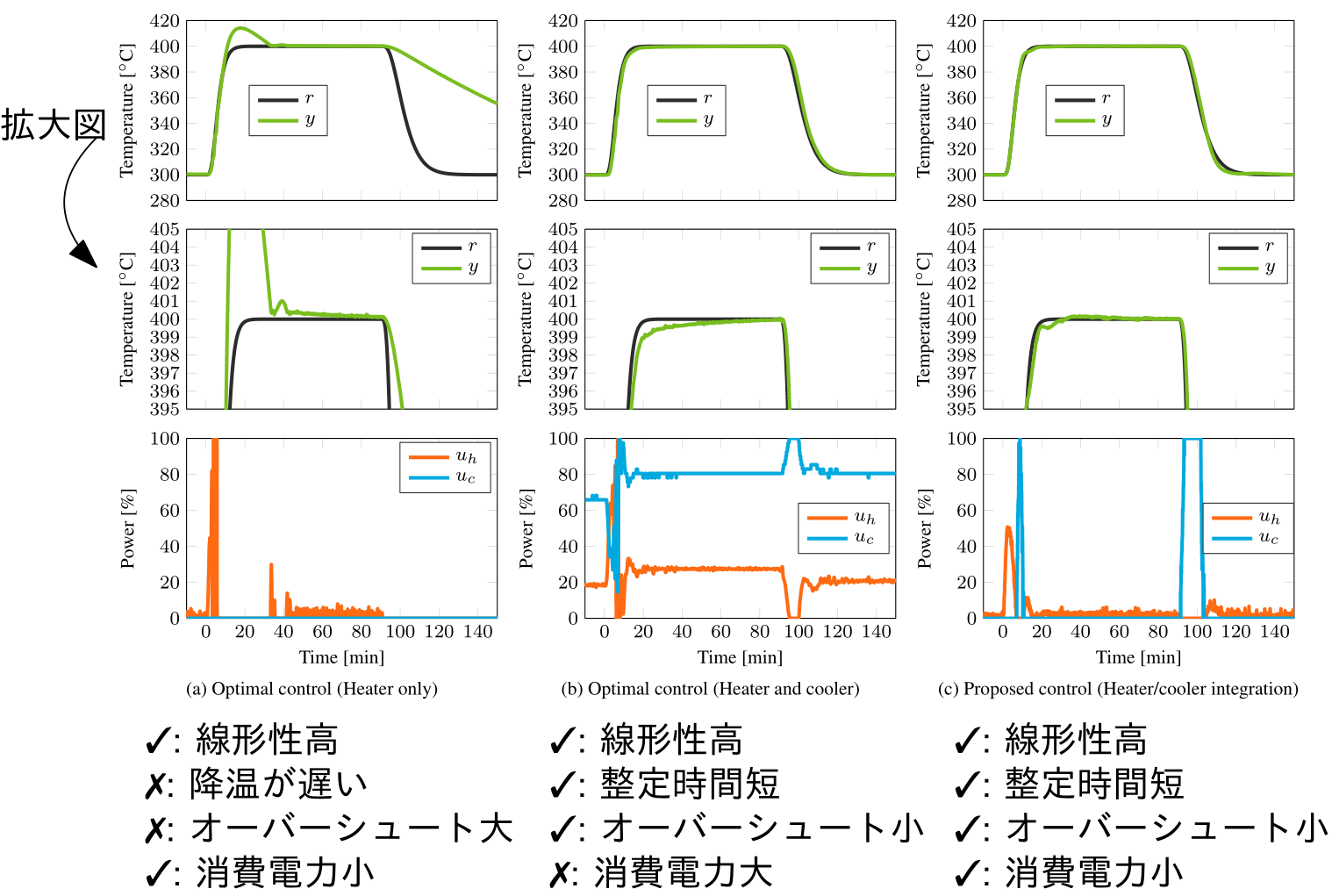
実験データは上図の通りで,提案手法は線形性,整定時間,オーバーシュート,消費電力いずれの指標からも良好な制御性能を達成しました。
新型遮断器により高圧直流送電を実現する
再生可能エネルギー大量導入や,電気自動車への高速給電の普及に伴い,事故を遮断する直流遮断器の重要性は大幅に増しています。 しかし,1秒間に100回あるいは120回電流零点がある交流と異なり,直流は電流零点がないため,本質的に遮断が非常に難しいです。

そのため,定格以上のヒューズや半導体を用いようとすると,上図のように過負荷で爆発していまいます。そのため,半導体スイッチを多数直並列にする研究も行われていおり,実用化もされていますが,半導体のON抵抗のため発熱が大きく,大型の冷却装置が必要になるという欠点があります。
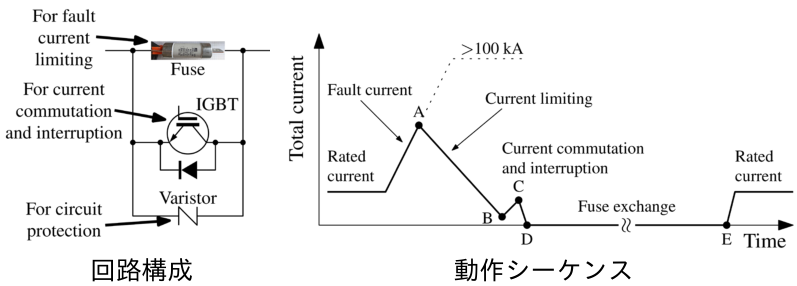
そこで,埼玉大学,東京工業大学,名古屋大学,金沢大学との共同研究で,リニアモータによるヒューズ高速切替機構を持つヒューズ・半導体ハイブリッド遮断器を提案しました。 これは,上図のような回路構成で,ヒューズ・半導体・バリスタが並列に接続され,かつヒューズに交換装置がついている構成となっています。
定格運転時は,半導体がOFFであり,ヒューズに定格電流が流れます。このとき,ヒューズのON抵抗は半導体スイッチのON抵抗よりもはるかに少ないため,冷却装置が不要であるという利点があります。
事故電流遮断時は,まずヒューズにより事故電流が限流(ヒューズの抵抗増大による電流制限)され,少電流となったあとに,半導体スイッチ(例えばIGBT)をONします。そうすると,ヒューズを流れていた少電流の事故電流は半導体を流れ(転流),これによりヒューズが冷却されて絶縁体になります。そしてヒューズが冷却されたタイミングで半導体をOFFすると事故電流が遮断されます。このときの過渡回復電圧はバリスタが保護します。そして使用済みのヒューズはリニアモータにより高速転換されることで,再閉路に備えます。
本構成の画期的なところは,それぞれの欠点を補い合いながら,利点を活かし合う構成になっているということです。ヒューズは電流の限流は得意なものの,直流電流の完全な遮断は不得手であり,さらに使い捨てという根本的な課題があります。また,半導体スイッチは電流の完全な遮断は得意なものの,定格電流と事故電流の大電流化には多大なコストがかかります。遮断容量点においてヒューズと半導体が補い合い,さらにヒューズが使い捨てという欠点はヒューズ取替機構によって解決されています。
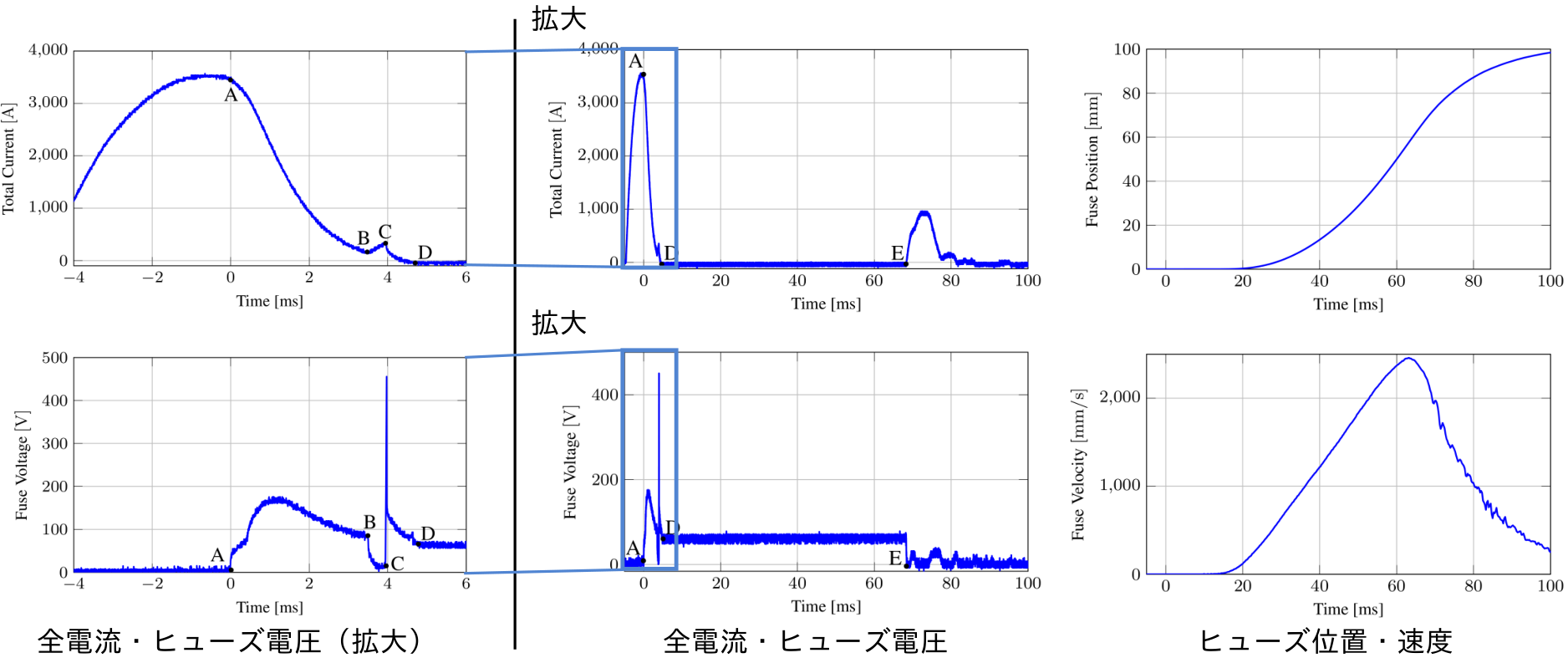
実験結果は上図で,3kAを超える事故電流の限流,遮断,保護,ヒューズ交換が成功していることがわかります。本プロジェクトは,NEDO未踏チャレンジ2050に採択されています。